Efficient sparse octree

In this post I am going to explain how I have implemented an efficient, pointer-less, and cache-friendly memory layout for an octree structure, written in C++.

Purpose of the octree

I needed to create a very fast octree structure for my game engine. It is primarily used for pathfinding in a 3D open space, building spaceships from blocks, and many other things. In these situations I needed very fast queries on whether a specific point is occupied or not, therefore, optimized for death-first search. Inserts could be slow, because they would be done once at the beginning of the game, or very infrequently.

The basics

The octree is stored in a linear memory std::vector<Node>. This is critical as it allows us to avoid costly memory allocations and a linear memory is better against cache misses (depending on the use-case).

First, let's start with the root.

The root is of type Branch, which is a union subtype of Node. Each branch has a property called next. The next is simply an integer that specifies a relative position of the next branch. Note, the #0 specifies position in the std::vector<Node>.

Because this is the root node, we know that the next node is pointing outside the array. We can ignore it.

Let's insert a leaf node.

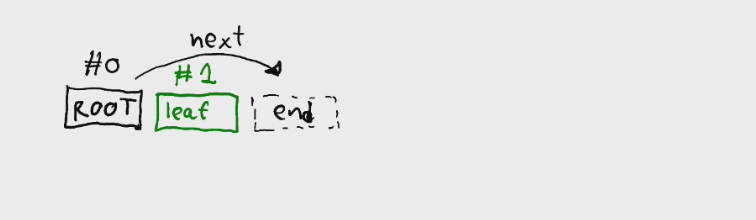
The new lead node is a child node of the root. It must be placed to the right of the parent, the root. The parent's next property is set to value of 2. This again points to the outside of the array.

If we ask a query whether a point is occupied, we start from the root, and we know that next value is 2, therefore, we know that there are some children.

The leaf node simply holds some value of type T.

Such structure looks like this:

union Node {
    struct Leaf {
        T value;
    } leaf;
    struct Branch {
        uint32_t next;
    } branch;
};

Now let's insert another child node to the root. A sibling node to the leaf node at #1.

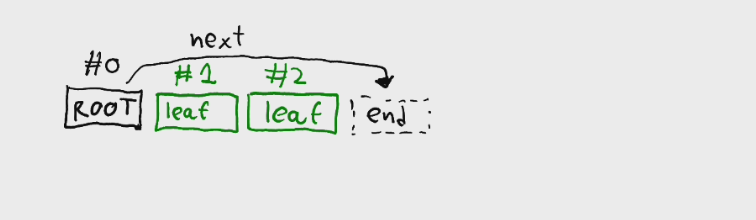
The process is the same as before. However, how do we know which octet the leaf node occupies? We need one more field into the Branch struct.

union Node {
    struct Leaf {
        T value;
    } leaf;
    struct Branch {
        uint8_t occupancy;  // <--- this!!
        uint32_t next;
    } branch;
};

We simply store the occupancy of the leaf nodes in the Branch struct's occupancy field. This is a bitfield, so we can store up to 8 bits of information, which is exactly the amount we need to store, 8 octants.

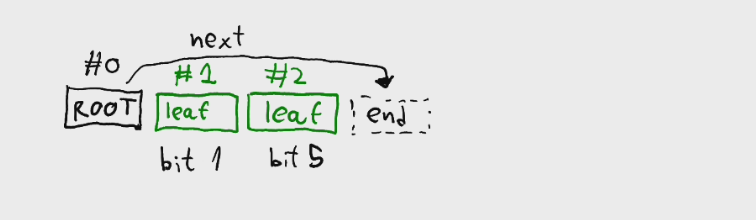
When looking for a node at a specific point, we have to traverse the tree recursively.

Such function looks like this:

template <typename T>
class Octree {
private:
  std::vector<Node> nodes = { // Start with a root node
    Branch{.occupancy = 0, .next = 1},
  };
  uint32_t depth = 1; // Start with a depth of 1
  
  /**
   * Returns the width of the octree at the given level.
   */
  int getWidthForLevel(const int level) {
      return static_cast<int>(std::pow<int>(2, level)) / 2;
  }
  
  bool isOutside(const Vector3i& pos) const {
      const auto w = getWidth();
      if (pos.x > w || pos.x <= -w)
          return true;
      if (pos.y > w || pos.y <= -w)
          return true;
      if (pos.z > w || pos.z <= -w)
          return true;
      return false;
  }
  
  /**
   * Given the current bifield bit position, and a value that represents
   * all of the occupied octants, returns the next bit position that is occupied.
   */
  uint8_t nextChildCode(uint8_t current, uint8_t value) {
      if (!value) {
          return current;
      }
  
      while ((value & 1 << current) == 0) {
          current++;
      }
  
      return current;
  }
  
  T* find(Node& node, const Vector3i& origin, const Vector3i& pos, int level) {
      // With of octant at the current node
      const auto w = getWidthForLevel(level);
      
      // Finds the bitfield index of the child node
      const auto childCode = octreePosToIndex(pos, origin);
      
      // Early exit if such child does not exist
      if ((node.branch.occupancy & (1 << childCode)) == 0) {
          return nullptr;
      }
      
      // Position within the memory of the parent node
      auto parentIdx = &node - nodes.data();
      
      // First sibling position
      auto siblingIdx = parentIdx + 1;
      
      // Pointer to the first sibling node
      auto* sibling = &nodes[siblingIdx];
      
      // Find the octant index of the first sibling
      size_t i = nextChildCode(0, node.branch.occupancy);
      
      // Iterate until we find the octant that contains the point
      while (i < childCode) {
          if (level == 1) {
              // We are at the bottom of the tree
              siblingIdx += 1;
          } else {
              siblingIdx += sibling->branch.next;
          }
          
          sibling = &nodes[siblingIdx];
          
          // Advance to the next sibling
          i = nextChildCode(i + 1, node.branch.occupancy);
      }
      
      if (level == 1) {
          // We are at the bottom of the tree
          return &sibling->leaf.value;
      }
      
      // Shift the origin to the center of the child octant
      const auto childOrigin = origin - octreeOffsets[7 - childCode] * w / 2;
      
      // Continue recursively until we are at the bottom of the tree
      return find(*sibling, childOrigin, pos, level - 1);
  }
  
public:
  /**
   * Returns the width of the entire octree.
   */
  int getWidth() const {
      return getWidthForLevel(depth);
  }
  
  T* find(const Vector3i& pos) {
      if (isOutside(pos)) { // Whether the point is outside the octree
          return nullptr;
      }
      return find(nodes[0], Vector3i{0, 0, 0}, pos, depth); // Start at level=depth
  }
};